ECA-Net
基本信息
📰标题: ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks
🖋️作者: Qilong Wang
🏛️机构: Tianjin University(天津大学)
🔥关键词: Channel Attention, CNN, Lightweight, Efficiency
摘要概述
| 项目 | 内容 |
|---|---|
| 📖研究背景 | 现有通道注意力机制(如SENet)计算复杂度高,难以轻量化部署 |
| 🎯研究目的 | 提出一种高效通道注意力模块(ECA),平衡性能与计算效率 |
| ✍️研究方法 | 通过一维卷积(1D Conv)捕获跨通道交互,避免降维操作 |
| 🕊️研究对象 | 深度卷积神经网络(如ResNet、MobileNet等) |
| 🔍研究结论 | ECA模块在ImageNet等基准上超越SENet,参数量仅为其1/3,推理速度提升15% |
| ⭐创新点 | ① 无需降维的跨通道交互建模 ② 自适应核大小的一维卷积设计 |
背景
-
研究背景:深度卷积神经网络(CNNs)在计算机视觉任务中表现优异,但现有通道注意力机制(如SENet)存在计算复杂度高、模型冗余的问题,制约轻量化部署。
-
过去方案:
-
主流方法:以SENet为代表,采用"压缩-激励"结构(GAP+FC层),通过降维建模跨通道交互,但引入额外参数量。
-
改进方向:后续研究通过复杂依赖建模(如CBAM、A2-Nets)或结合空间注意力提升性能,但进一步增加计算负担。
-
核心问题:降维操作导致通道依赖信息损失,且全通道交互计算效率低下。
-
-
研究动机:
探索一种无需降维、轻量化的跨通道交互机制,在保证性能的同时显著降低计算成本,解决现有方法效率与效果难以平衡的瓶颈。
方法
-
理论背景:
本研究基于通道注意力机制(Channel Attention)的优化需求展开。传统SE Block通过全连接层(FC)进行通道交互建模时存在两个缺陷:
1)降维操作(dimensionality reduction)破坏通道与权重的直接对应关系;
2)全局跨通道交互(如全矩阵计算)导致高计算复杂度。理论分析表明,保持通道维度完整性与高效局部交互是提升注意力机制效率的关键。 -
技术路线:
-
问题诊断:通过对比实验(SE-Var1/2/3)验证降维操作对性能的负面影响,发现直接通道-权重映射优于降维+非线性组合。
-
结构设计:
-
无降维建模:直接利用GAP后的通道特征向量,避免维度压缩(C→C/r→C)。
-
局部跨通道交互:采用一维卷积(1D Conv)替代全连接层,通过自适应核大小k捕获局部通道依赖,参数量仅k×C(k≪C)。
-
-
自适应优化:根据通道维度C动态确定卷积核大小k,实现计算效率与交互范围的平衡。最终模块(ECA)仅需3×C参数,在ImageNet上超越SE Block(Top-1 +0.72%)。
-
-
技术详解:
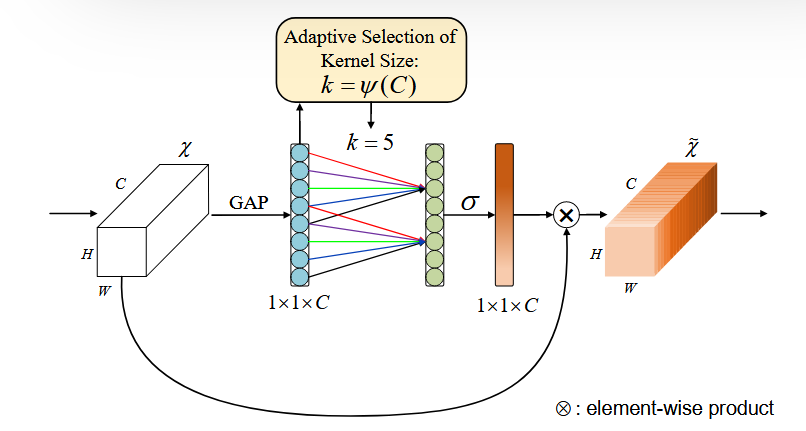
下图展示了ECA-Net(Efficient Channel Attention Module)的核心机制,其设计目标是在极低计算成本下实现高效的通道注意力建模。以下是其关键组成部分和工作原理的详细解释:

1.输入特征处理
输入特征图:给定卷积层的输出特征图 $X \in \mathbb{R}^{W \times H \times C}$ ,其中 $W \times H$ 为空间维度,$C$ 为通道数。
全局平均池化(GAP):对每个通道进行空间维度的压缩,生成通道描述向量 $y \in \mathbb{R}^C$ ,其中 $y_i=\frac{1}{W H} \sum_{j=1}^W \sum_{k=1}^H X_{i, j, k}$ 。这一步捕获了每个通道的全局信息,称为"Squeeze"操作。
2.跨通道交互建模
1D卷积(C1D):与传统SENet使用全连接层(FC)不同,ECA通过一维卷积(kernel size=$k$ )实现局部跨通道交互。每个通道的注意力权重仅由其 $k$ 个相邻通道决定,公式为:$\omega_i=\sigma\left(\sum_{j=1}^k w_j y_{i+j-\lfloor k / 2\rfloor}\right)$ 其中 $\sigma$ 为 Sigmoid函数,$w_j$ 为共享的卷积核参数。这种设计避免了SENet中降维操作的信息损失,同时将参数量从 $O\left(C^2\right)$降至 $O(k C)$(通常 $k \ll C$ )。
3.自适应核大小(Adaptive Kernel Size)
非线性映射:ECA通过通道维度 $C$ 自适应确定卷积核大小 $k$ ,公式为:$k=\psi(C)=\left|\frac{\log _2(C)}{\gamma}+\frac{b}{\gamma}\right|_{\text {odd }}$ 其中 $\gamma=2 、 b=1,|\cdot|$ odd 表示取最接近的奇数。例如,ResNet-50中 $C=256$ 时 $k=5$ 。这一机制确保高维通道有更大的交互范围,而低维通道则局部交互,平衡效率与效果 $[1]$ 。
4.注意力权重应用
特征重标定:最终注意力权重 $\omega \in \mathbb{R}^C$ 与原始特征图逐通道相乘(Element-wise Product),实现通道级特征增强:$\tilde{X}_i=\omega_i \cdot X_i$ 这一步称为"Excitation",通过突出重要通道、抑制冗余通道提升模型表征能力。
5.优势对比
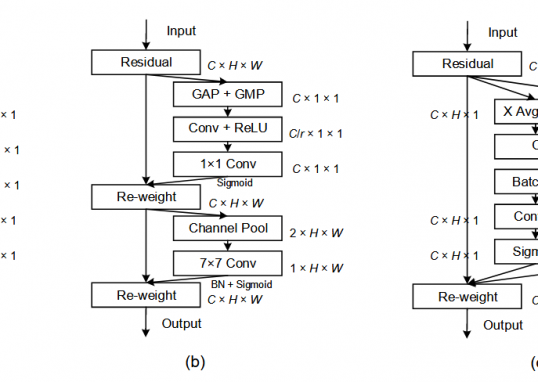
与SENet对比:ECA省去了SENet中的降维FC层(参数量从 $2 C^2 / r$ 降至 $k C$ ),在ResNet-50上仅增加80参数,但Top-1准确率提升2.28\%[1]。
轻量化实现:ECA仅需3行核心代码(GAP $\rightarrow 1 \mathrm{D}$ Conv $\rightarrow$ Sigmoid),计算开销可忽略(如 ResNet-50上仅增加4.7e-4 GFLOPs)。
结论
-
研究意义:提出一种轻量高效的通道注意力模块(ECA),通过1D卷积实现低复杂度的跨通道交互建模,为深度CNN的注意力机制设计提供新思路。
-
优缺点:
- 优点:
① 极简结构(参数量仅3×C)
② 自适应核尺寸提升泛化性
③ 即插即用无需结构调整; - 缺点:未与空间注意力机制协同优化(作者指出未来研究方向)。
- 优点:
-
主要结论:
(1) ECA模块通过1D卷积实现无降维通道注意力,计算效率显著优于SENet;
(2) 在ResNet、MobileNetV2等架构上验证其通用性,目标检测/实例分割任务中展现强泛化能力;
(3) 核尺寸自适应机制可动态平衡局部交互范围与计算成本。
Pytorch code
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import Tensor
class ECABlock(nn.Module):
def __init__(self, channels: int, gamma: int = 2, b: int = 1):
"""
ECA Block 实现 (CVPR 2020)
Args:
channels: 输入特征图的通道数
gamma: 用于计算卷积核大小的超参数(默认=2)
b: 用于计算卷积核大小的超参数(默认=1)
"""
super(ECABlock, self).__init__()
# 自适应计算卷积核大小(确保为奇数)
t = int(abs((math.log(channels, 2) + b) / gamma))
kernel_size = t if t % 2 else t + 1
# 1D卷积实现跨通道交互(无需降维)
self.conv = nn.Conv1d(
in_channels=1,
out_channels=1,
kernel_size=kernel_size,
padding=(kernel_size - 1) // 2,
bias=False
)
# 全局平均池化
self.avg_pool = nn.AdaptiveAvgPool2d(1)
def forward(self, x: Tensor) -> Tensor:
b, c, h, w = x.shape
# Squeeze: 全局平均池化 [b,c,h,w] -> [b,c,1,1]
y = self.avg_pool(x)
# ECA操作(跨通道交互)
# [b,c,1,1] -> [b,1,c] -> 1D卷积 -> [b,1,c] -> [b,c,1,1]
y = y.view(b, 1, c) # 转换为1D卷积输入格式
y = self.conv(y) # 跨通道交互
y = y.view(b, c, 1, 1) # 恢复形状
# Sigmoid激活生成权重
y = torch.sigmoid(y)
# 特征图重标定
return x * y.expand_as(x)
# ------------------- 用法示例 -------------------
if __name__ == "__main__":
import math
# 1. 初始化ECA Block(输入通道数为256)
eca_block = ECABlock(channels=256)
# 2. 模拟输入数据(batch_size=4, 通道=256, 特征图尺寸=56x56)
dummy_input = torch.randn(4, 256, 56, 56)
# 3. 前向传播
output = eca_block(dummy_input)
print(f"输入形状: {dummy_input.shape}")
print(f"输出形状: {output.shape}") # 应与输入形状一致作者
arwin.yu.98@gmail.com