Pyramid Vision Transformer
基本信息
-
📰标题: Pyramid Vision Transformer: A Versatile Backbone for Dense Prediction without Convolutions
-
🖋️作者: Wenhai Wang
-
🏛️机构: Nanjing University(南京大学)
-
🔗链接: GitHub
-
🔥关键词: Pyramid Vision Transformer, Dense Prediction, Backbone, Convolution-free
摘要概述
| 项目 | 内容 |
|---|---|
| 📖研究背景 | CNN骨干网络普遍采用金字塔结构处理密集预测任务,而ViT仅针对图像分类设计 |
| 🎯研究目的 | 将金字塔结构引入ViT,构建适用于多任务的通用卷积-free骨干网络 |
| ✍️研究方法 | 提出Pyramid Vision Transformer (PVT),融合CNN金字塔结构与Transformer编码器 |
| 🕊️研究对象 | 密集预测任务(如目标检测、实例/语义分割) |
| 🔍研究结论 | PVT显著扩展ViT应用范围,可与DETR结合构建端到端无卷积检测系统 |
| ⭐创新点 | 1) 首个金字塔式Transformer骨干网络 2) 兼容密集预测任务 3) 完全无卷积设计 |
背景
-
研究背景:
CNN在计算机视觉领域占据主导地位,但存在局部感受野的固有局限。ViT虽在图像分类中表现优异,但其单尺度、低分辨率输出及高计算成本难以适配密集预测任务(如目标检测、分割)。 -
过去方案:
-
CNN骨干网络(如ResNet、ResNeXt):依赖局部感受野,需手动设计锚框/NMS等组件;
-
Transformer改进方案:
-
混合架构(如ViT+CNN):仍依赖卷积操作,非纯Transformer设计;
-
原生ViT:因粗粒度图像分块(32×32像素)导致输出分辨率低,无法支持像素级预测。\
核心问题:缺乏兼具金字塔结构、全局感受野与计算效率的纯Transformer骨干网络。
-
- 研究动机:
构建首个完全无卷积的金字塔式Transformer骨干网络(PVT),通过细粒度分块(4×4像素)、渐进式金字塔缩减及空间缩减注意力(SRA),解决ViT在密集预测任务中的多尺度特征缺失与计算瓶颈,实现端到端无手工组件的检测系统(如PVT+DETR)。
方法
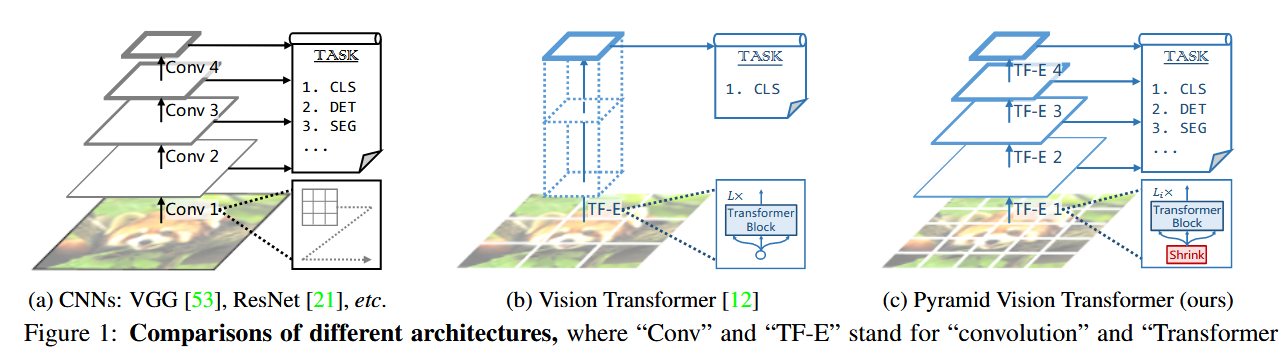
图1通过三栏对比了 CNN(ResNet)、 ViT 和 PVT 的结构差异:
1.CNN(左栏):
- 展示ResNet的4阶段金字塔结构,每个阶段通过卷积 stride $=2$ 降采样。
- 特征图尺寸从 $\frac{H}{4} \times \frac{W}{4}$ 逐步降至 $\frac{H}{32} \times \frac{W}{32}$ 。
2.ViT(中栏):
- 单一尺度处理:输入图像被分为 $16 \times 16$ 的块,通过Transformer编码器后输出固定分辨率的序列。
- 缺乏多尺度特征,需额外上采样才能用于密集预测任务。
3.PVT(右栏):
- 类似CNN的4阶段金字塔结构,但用 Patch Embedding 和 Transformer Encoder 蒈代卷积。
- 每个阶段标注了输出分辨率 $\left(\frac{H}{4}\right.$ 到 $\left.\frac{H}{32}\right)$ 和通道数 $\left(C_1\right.$ 到 $\left.C_4\right)$ 。
技术意义
1.多尺度能力:
PVT通过分阶段降采样保留金字塔结构,解决了ViT的单一尺度缺陷,可直接用于目标检测/分割。
2.纯Transformer设计:
与CNN不同,PVT完全依赖自注意力机制,避免了卷积的局部性限制[1,Sec.1]。
3.即插即用性:
图示表明PVT的输出格式与ResNet完全兼容(多尺度特征图),可直接替换CNN等骨干网络。
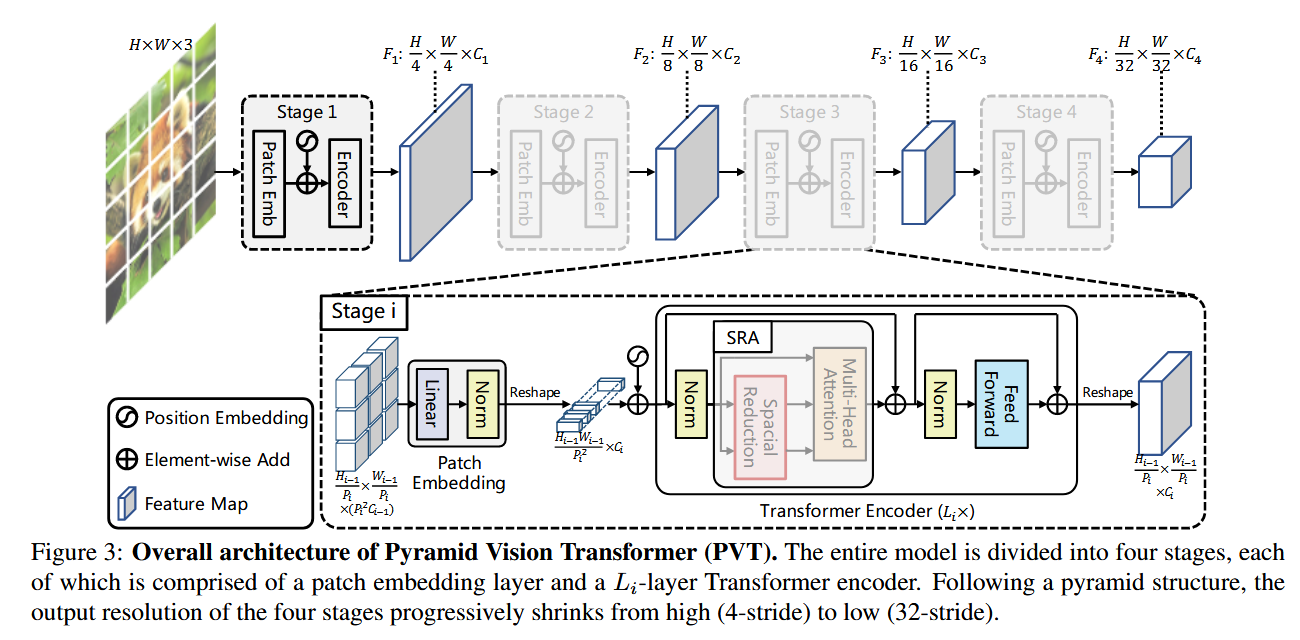
图3展示了PVT中 单个Transformer Encoder层 的详细结构,包含两个核心模块:
1.Spatial-Reduction Attention(SRA):
- Query $(Q)$ 保持原始分辨率,与所有位置交互,保持了全局建模能力。
- $\operatorname{Key}(K)$ 和 Value( $V$ )通过 空间缩减(SR)模块 降采样(标注了缩减比 $R$ )。
- 注意力矩阵计算为 $\operatorname{Softmax}\left(Q K^T / \sqrt{d}\right) V$ ,但 $K, V$ 的分辨率降低至 $\frac{H}{R} \times \frac{W}{R}$ 。
2.前馈网络(FFN):
标准的两层MLP,中间扩展比为4(与ViT一致)。

SRA的核心动机
传统Transformer的多头自注意力(MSA)在视觉任务中面临两大问题:
-
计算复杂度高:MSA对序列长度 $N=H \times W$ 的复杂度为 $O\left(N^2\right)$ ,高分辨率输入,计算资源消耗过大。
-
空间信息冗余:相邻像素的Key/Value高度相似,直接计算全局注意力存在大量重复运算。
SRA的算法实现
SRA通过降采样Key/Value显著降低计算量,同时保留全局感受野。给定输入特征 $X \in \mathbb{R}^{H \times W \times C}$ ,SRA按以下步骤处理:
- 生成 $Q / K / V$ :
。 $Q=X W_Q \in \mathbb{R}^{H \times W \times d_k} \quad$(保持原始分辨率)
-$K, V$ 先通过 空间缩减(Spatial Reduction,SR)降采样:
$$
K_{\text {reduced }}=\operatorname{SR}\left(X W_K\right), \quad V_{\text {reduced }}=\operatorname{SR}\left(X W_V\right)
$$
2.计算注意力: $\operatorname{Attention}(Q, K, V)=\operatorname{Softmax}\left(\frac{Q K_{\text {reduced }}^T}{\sqrt{d_k}}\right) V_{\text {reduced }}$
空间缩减(SR)的数学表达
SR操作包含两步:
- 均匀池化下采样:
将 $K, V \in \mathbb{R}^{H \times W \times C}$ 按缩减比 $R$ 划分网格,每个 $R \times R$ 区域取均值或最大值:
Reshape $(K) \in \mathbb{R}^{\frac{H}{R} \times R \times \frac{W}{R} \times R \times C} \rightarrow$ Pooling $\rightarrow \mathbb{R}^{\frac{H}{R} \times \frac{W}{R} \times C}$ - 线性投影:
通过可学习权重 $W_S \in \mathbb{R}^{C \times C^{\prime}}$ 调整维度: $\operatorname{SR}(K)=\operatorname{Norm(Reshape(K)W_{S})\text {(Norm通常为Layer}}$
Normalization)
复杂度分析
-原始MSA:$O\left(N^2\right)=O\left((H W)^2\right)$
-SRA:$O\left(\frac{(H W)^2}{R^2}\right)$
例如当 $R=8$ 时,计算量降至 $1 / 64$ 。
(论文中PVT-Small的Stage 4设置 $R=8$ )
结论
-
本研究提出了首个纯Transformer架构的金字塔骨干网络PVT,通过渐进式收缩金字塔和空间缩减注意力(SRA)机制,解决了ViT在密集预测任务中的多尺度特征缺失与计算瓶颈问题,为计算机视觉领域提供了CNN之外的替代性基础架构。
-
优点:
-
完全无卷积设计,实现端到端全局建模;
-
在参数量可比条件下性能超越主流CNN骨干(如ResNet);
-
SRA机制显著降低计算复杂度(降至O(N²/R²))。
-
-
主要结论:
- PVT通过渐进式金字塔和SRA层,可在有限计算资源下生成高分辨率多尺度特征;
- 在目标检测和语义分割任务中,PVT性能优于同参数量CNN骨干;
- 作为Transformer在CV领域的早期探索,PVT为OCR、3D视觉和医学图像等方向提供了可扩展的基础框架。
作者
arwin.yu.98@gmail.com