Non-local Neural Networks
基本信息
- 📰标题: 非局部神经网络(Non-local Neural Networks)
- 🖋️作者: Xiaolong Wang
- 🏛️机构: Carnegie Mellon University(卡内基梅隆大学)
- 🔥关键词: Non-local operations, self-attention, video recognition, image classification
摘要概述
| 项目 | 内容 |
|---|---|
| 📖 研究背景 | 传统深度卷积网络难以建模长距离依赖关系 |
| 🎯 研究目的 | 提出通用非局部运算模块,捕获时空远程依赖 |
| ✍️ 研究方法 | 设计非局部算子(含4种变体),结合残差连接 |
| 🕊️ 研究对象 | 视频动作识别(Kinetics)与图像分类(ImageNet) |
| 🔍 研究结论 | 在视频分类任务中提升1.5%准确率(优于3D卷积) |
| ⭐ 创新点 | 首次将非局部均值思想扩展为可微分神经网络组件 |
背景
-
研究背景:深度神经网络中长程依赖建模是关键挑战,现有方法在时空数据(如视频、图像)中存在显著局限性。
-
过去方案:
-
RNN:适用于序列数据但存在梯度消失/爆炸问题
-
CNN:依赖深层堆叠扩大感受野,计算效率低且优化困难
-
核心缺陷:局部操作的重复累积导致多跳依赖建模失效(如远距离像素间双向交互)
-
-
研究动机:
-
提出可微分non-local operations,直接建模任意位置间全局依赖
-
突破传统卷积/循环结构的渐进式特征传播局限,建立跨时空的一步交互机制
-
通过统一框架兼容图像/视频/序列任务,验证其在视频分类(Kinetics)和COCO多任务中的泛化性
-
方法
-
理论背景:
基于传统卷积神经网络在长程依赖建模中的局限性,研究借鉴非局部均值滤波(non-local means)思想,将图像处理中的非局部相似性计算扩展为可微分神经网络算子。该工作受self-attention机制启发,但突破其序列建模限制,提出适用于时空数据的通用交互范式。 -
技术路线:
-
算子设计:构建非局部运算模块( $\mathcal{NL}(·)$ ),通过高斯核函数计算任意两点间关联权重,支持Embedded Gaussian/Dot Product/Concatenation等4种相似度计算变体
-
结构实现:
-
采用残差连接形式( $\mathbf{z}_i = \mathcal{NL}(\mathbf{x}_i) + \mathbf{x}_i$ )避免梯度消失
-
通过1×1卷积压缩特征维度降低计算复杂度
-
-
任务适配:
- 视频任务中直接处理3D特征图(T×H×W)
- 图像任务中通过空间位置映射实现全局上下文建模
-
-
详细解读:
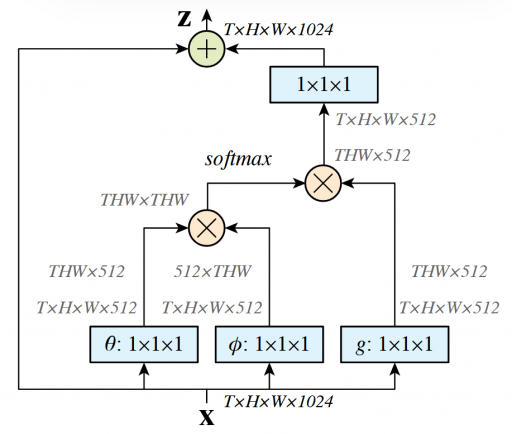
非局部神经网络(Non-local Neural Networks)的图解如下:
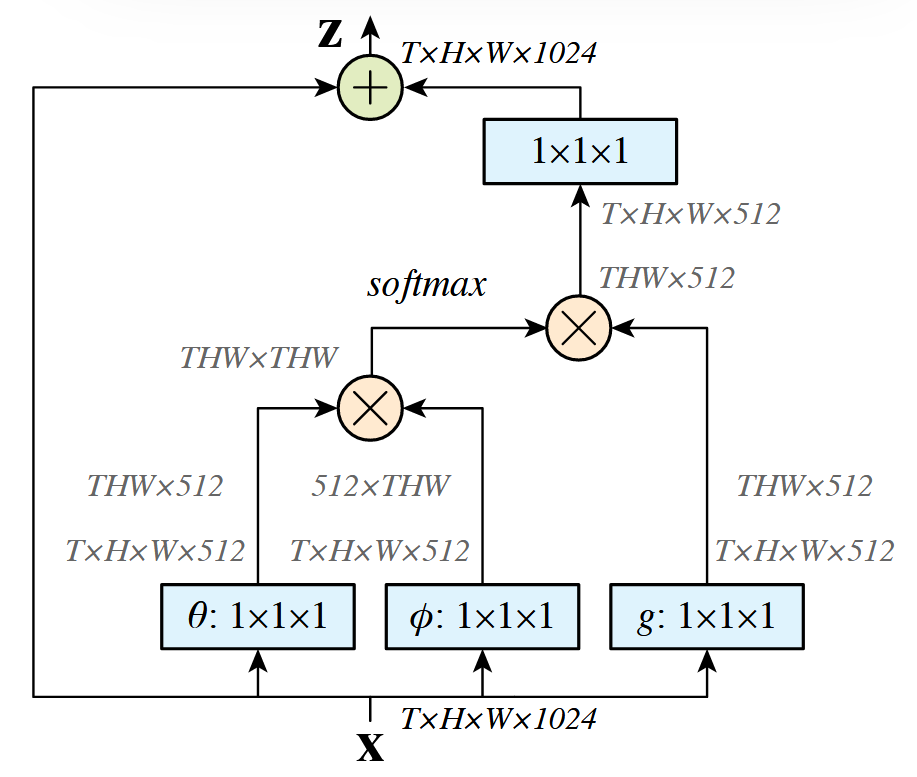
核心公式表示如下:
$$
y_i=\frac{1}{C(x)} \sum_{\forall j} f\left(x_i, x_j\right) g\left(x_j\right)
$$
公式组成解析
1.输入与输出
- $x$ :输入特征(图像/视频/序列),$y$ :与 $x$ 同尺寸的输出
- $i$ :目标位置索引(空间/时间/时空),$j:$ 枚举所有可能位置的索引
2.核心函数
- 相似性函数 $f\left(x_i, x_j\right)$ :计算位置 $i$ 与所有位置 $j$ 的关联权重(标量),支持四种变体:
- 高斯函数:$f\left(x_i, x_j\right)=e^{x_i^T x_j}$(经典非局部均值滤波扩展)
- 嵌入高斯:$f\left(x_i, x_j\right)=e^{\theta\left(x_i\right)^T \phi\left(x_j\right)} \quad(\theta 、 \varphi$ 为线性嵌入,与自注意力机制等效)
- 点积:$f\left(x_i, x_j\right)=\theta\left(x_i\right)^T \phi\left(x_j\right)$(无softmax,归一化因子 $C(x)=N$ )
- 拼接:$f\left(x_i, x_j\right)=\operatorname{ReLU}\left(w_f^T\left[\theta\left(x_i\right), \phi\left(x_j\right)\right]\right)$.
- 特征变换函数 $g\left(x_j\right)$ :线性嵌入 $g\left(x_j\right)=W_g x_j \quad$(通过 $1 \times 1$ 卷积实现)
- 归一化因子 $C(x)$ :通常取 $\sum_{\forall j} f\left(x_i, x_j\right)$ 或样本数 $N$
3.残差连接设计
非局部块(Non-local Block)通过残差连接整合输出:$z_i=W_z y_i+x_i$
- $W_z$ 为可学习权重矩阵,初始化为零以保持初始行为
- 残差结构允许直接插入预训练模型而不破坏其性能
结论
-
提出非局部运算(non-local operations)作为建模长程依赖的新范式,为神经网络架构设计提供通用组件,在视频理解与图像分析多任务中验证其普适价值
-
优点:
-
模块化设计兼容现有架构(如CNN/RNN)
-
在视频分类、目标检测、姿态估计等任务中均带来稳定性能提升\
局限: -
未讨论计算复杂度与实时性权衡
-
多任务泛化性需更多基准测试验证
-
-
主要结论:
(1) 非局部模块通过直接建模任意位置间依赖关系,显著优于传统局部运算的累积效应
(2) 该组件以即插即用方式提升视频分类等任务的baseline性能
(3) 预示非局部层(non-local layers)将成为未来网络架构的核心要素
Non-local Networks VS Transformer
非局部神经网络(Non-local Networks)确实可以视为Transformer的“近亲”,两者在核心思想和技术路线上高度相似,但存在一些关键差异。以下是详细对比分析:
| 维度 | 非局部网络(2018) | Transformer(2017) |
|---|---|---|
| 基础思想 | 通过全局交互建模长程依赖 | 通过自注意力机制捕获序列内任意位置的关联 |
| 数学形式 | \(y_i=\sum_j \operatorname{softmax}\left(x_i^T x_j\right) g\left(x_j\right)\) | \(y_i=\sum_j \operatorname{softmax}\left(Q K^T\right) V\) |
| 归一化方式 | 可选softmax或直接点积 | 必须使用softmax |
| 残差设计 | \(z_i=W_z y_i+x_i\) | LayerNorm(\(x+\operatorname{Attention}(x)\)) |
历史脉络
- 2017年:Vaswani等提出Transformer,但最初仅用于NLP
- 2018年:Wang等提出非局部网络,首次将注意力式操作系统引入视觉任务
- 2020年后:ViT证明纯Transformer在视觉中可行,非局部网络的思想被Transformer架构吸收
如何理解两者的关系?
- 非局部网络 ≈ 视觉领域的“单头自注意力”
可以看作是为CNN定制的简化版Transformer模块,保留了空间结构 inductive bias。 - Transformer → 更通用的非局部操作
通过多头机制、层归一化等设计,形成了更强大的通用架构。
可视化理解(以视频任务为例)

- 输入:视频帧序列(T×H×W×C)
- 非局部操作:
- 计算第 $t$ 帧某像素与所有帧所有像素的关联权重(时空全局)
- 输出聚合后的特征(如点$x_i$位置增强与远处球$x_j$的关联)
- CNN后续处理:卷积层进一步融合局部-全局信息。
Pytorch code
import torch
import torch.nn as nn
import torch.nn.functional as F
class NonLocalBlock(nn.Module):
def __init__(self, in_channels, inter_channels=None, sub_sample=True, mode='embedded'):
"""
Non-local Block 实现
Args:
in_channels: 输入特征图的通道数
inter_channels: 中间特征通道数(默认为in_channels//2)
sub_sample: 是否在分支中使用最大池化进行下采样
mode: 非局部操作类型,可选 'embedded'/'dot'/'concatenate'
"""
super(NonLocalBlock, self).__init__()
self.mode = mode
self.in_channels = in_channels
self.inter_channels = inter_channels if inter_channels is not None else in_channels // 2
# 定义各分支的卷积层
self.g = nn.Conv2d(in_channels, self.inter_channels, kernel_size=1)
self.theta = nn.Conv2d(in_channels, self.inter_channels, kernel_size=1)
self.phi = nn.Conv2d(in_channels, self.inter_channels, kernel_size=1)
# 输出转换层
self.W = nn.Conv2d(self.inter_channels, in_channels, kernel_size=1)
nn.init.constant_(self.W.weight, 0)
nn.init.constant_(self.W.bias, 0)
# 下采样相关
self.sub_sample = sub_sample
if sub_sample:
self.g = nn.Sequential(self.g, nn.MaxPool2d(kernel_size=2))
self.phi = nn.Sequential(self.phi, nn.MaxPool2d(kernel_size=2))
def forward(self, x):
"""
前向传播
Args:
x: 输入特征图 [batch, channels, height, width]
Returns:
经过non-local操作的特征图 [batch, channels, height, width]
"""
batch_size = x.size(0)
# g分支
g_x = self.g(x).view(batch_size, self.inter_channels, -1)
g_x = g_x.permute(0, 2, 1)
# theta分支
theta_x = self.theta(x).view(batch_size, self.inter_channels, -1)
theta_x = theta_x.permute(0, 2, 1)
# phi分支
phi_x = self.phi(x).view(batch_size, self.inter_channels, -1)
# 计算注意力图
f = torch.matmul(theta_x, phi_x)
f = F.softmax(f, dim=-1)
# 注意力加权
y = torch.matmul(f, g_x)
y = y.permute(0, 2, 1).contiguous()
y = y.view(batch_size, self.inter_channels, *x.size()[2:])
# 输出转换
z = self.W(y)
return z + x # 残差连接
# ------------------- 用法示例 -------------------
if __name__ == "__main__":
# 1. 初始化Non-local Block(输入通道数为256)
nl_block = NonLocalBlock(in_channels=256, mode='embedded')
# 2. 模拟输入数据(batch_size=4, 通道=256, 特征图尺寸=56x56)
dummy_input = torch.randn(4, 256, 56, 56)
# 3. 前向传播
output = nl_block(dummy_input)
print(f"输入形状: {dummy_input.shape}")
print(f"输出形状: {output.shape}") # 应与输入形状一致作者
arwin.yu.98@gmail.com