ClofNet

1、局部坐标系

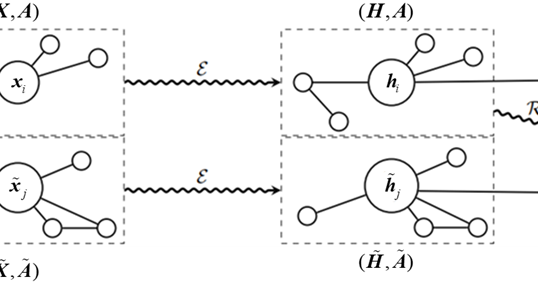
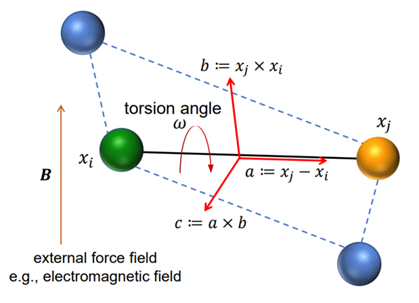
ClofNet的作者指出，在传统的等变几何GNN表征框架中（例如EGNN），通常只考虑了原子或粒子之间的相对位置来描述它们的相互作用，这种方法并没有考虑到外部条件，如恒定电场对粒子间相互作用的影响。在一个恒定电场中，电场对粒子的作用是一个固定方向的向量，这对所有粒子都是一样的，并且与它们的相对位置无关。因此，ClofNet提出了局域坐标系的解决方案，这个坐标系不仅能够捕捉粒子间的相对位置，还能够包含其他的物理因素，如电场方向，局域坐标系具体的定义方法如图1所示。

如图1所示，考虑了一个多体系统中的两体子系统\((x_i,x_j)\)，这个系统不随时间变化，可以被看作是一个具有两个节点和一条边的图。一般而言，两个粒子间的相互作用函数可以分解成两部分：\(U\left(x_{i},x_{j}\right):=U_{\mathrm{in}}\left(\parallel x_{i}-x_{j}\parallel\right)+U_{\mathrm{ext}}\left(x_{i},x_{j}\right)\) ，其中第一部分是相对距离\(\left|x_i-x_j\right|\)的函数（例如电静力)，第二部分描述了可能取决于相对距离和角度（例如电磁场、扭力）的外部力场的影响。因此，\(U_{\mathrm{ext}}\left(x_i,x_j\right)\)的梯度可以沿着任意方向在3D空间中发散。大多数几何GNN方法在处理这种力预测问题时，都是通过采用不变特征（例如，相对距离）作为输入，并表示沿径向的力，即\(F_{i}=k\left(x_{i}-x_{j}\right)\)，这在梯度\(\nabla U_{\mathrm{ext}}(x_i,x_j)\)不是沿着径向时是不够的。为了解决这个问题，clofNet提出了一个正交的等变局部坐标系框架（一种正交基组），用于构建和表示几何数据更完备的局部结构。具体来说，取\(x_{i}-x_{j}\)作为第一个分量/方向\(\mathrm{a}\)，然后\(x_i\times x_j\)作为第二方向\(\mathrm{b}\)。最后，前两个方向的叉积被作为第三方向\(\mathrm{c}\)。这三个向量\(\mathrm{a}\),\(\mathrm{b}\)和\(\mathrm{c}\) 定义了一个局部坐标系，由于叉乘的性质，\(\mathrm{b}\)垂直于\(\mathrm{a}\)，\(\mathrm{c}\)垂直于\(\mathrm{a}\)和\(\mathrm{b}\) 。换句话说，这个坐标系具有正交性。

2、clofNet模型总体架构

clofNet模型处理数据的流程可以分为中心化（Centralization）、局部完备框架（Complete Frame）、标量化（Scalarize）、消息传递模块（GMP）、向量化（Vectorize）和迭代更新六个步骤，如图2所示。

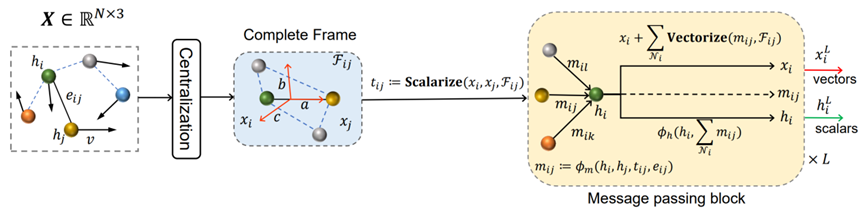
针对输入数据，模型首先将每个点的位置进行中心化处理。这通常意味着会从每个位置向量中减去所有位置向量的平均值，以确保模型对平移保持不变。这是因为通过减去所有点位置向量的平均值，实际上是在重新定位整个系统的中心（质心）到原点（坐标系的中心）的距离。这样，模型就不会将任何特定的位置作为参考点，因此无论系统在空间中如何平移，模型的输出都将保持不变。

局部完备框架\(\mathcal{F}_{ij}\)就是上一小节解释的局部正交坐标系。具体来说，令\(a_{ij}^{t}=\frac{x_{i}(t)-x_{j}(t)}{\begin{Vmatrix}x_{i}(t)-x_{j}(t)\end{Vmatrix}}\)，则可以定义\(b_{ij}^{t}=\frac{x_{i}(t)\times x_{j}(t)}{\left|x_{i}(t)\times x_{j}(t)\right|}\)和\(c_{ij}^t=a_{ij}^t\times b_{ij}^t\)。这三个相互正交的基组可以构建一个\(SO(3)\)-等变框架\(\mathcal{F}{ij}:\mathrm{EquiFrame}\left(x_{i},x_{j}\right)=\left(a_{ij}^{t},b_{ij}^{t},c_{ij}^{t}\right)\)。实际操作中，我们添加一个小常数\(\epsilon\)到归一化因子中，以防\(x_{i}\)和\(x_{j}\)发生重合。

基于上述的局部完备框架\(\mathcal{F}_{ij}\)，可以将任意几何向量转换为\(SO(3)\)不变的标量值。具体方法是将几何向量投影到\(\mathcal{F}_{ij}\)的基组上，通过内积获得相应的系数，这些系数是不变标量，表示为\(t_{ij}=\left(x_{i}\cdot a_{ij}^{t},x_{i}\cdot b_{ij}^{t},x_{i}\cdot c_{ij}^{t}\right)\)，这就是几何向量标量化的步骤。

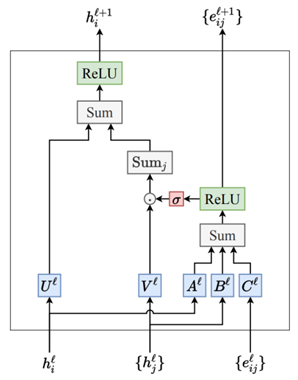
接下来，\(t_{ij}\)将与节点特征向量\(h_{i},h_{j}\)和边特征向量\(e_{ij}\)一起作为消息传递模块（GMP）的输入信息。GMP分为特征编码和信息传递两个信息处理阶段，特征编码阶段的处理非常简单，几何标量\(t_{ij}\)、节点特征\(h_{i},h_{j}\)和边特征\(e_{ij}\)分别经过神经网络层的处理，学习映射得到更新后的新特征表示。

在信息传递阶段，clofNet提出了朴素的消息传递和基于注意力的消息传递两种不同的机制。朴素的消息传递机制非常类似与模型EGNN。具体来说，将几何标量\(t_{ij}\)、节点特征\(h_{i},h_{j}\)和边特征\(e_{ij}\)同时作为一个神经网络层\(\phi_{_m}\)的输入，进行节点特征、边特征和几何特征之间的信息融合，计算得到新的特征向量\(m_{ij}\)，这个特征向量代表目标节点\(\mathrm{i}\)和其邻居\(\mathrm{j}\)之间的相互作用关系。因此，目标节点\(\mathrm{i}\)的特性更新方式就是对所有的邻居\(\mathrm{j}\)和其自身信息进行求和，并经过另一个神经网络层\(\phi_{h}\)计算得到，公式表示为：

\(\boldsymbol{m}_{ij}=\phi_{m}\left(s_{ij},\boldsymbol{h}_{i},\boldsymbol{h}_{j},\boldsymbol{e}_{ij}\right)
\)

\(\boldsymbol{h}_i^{l+1}=\phi_h\left(\boldsymbol{h}_i^l,\sum_{j\in\mathcal{N}(i)}\boldsymbol{m}_{ij}\right)\)

此外，与EGNN相似，clofNet也会对节点\(\mathrm{i}\)的位置信息\(x_{i}\)进行更新；不同的是EGNN的更新方式是直接基于笛卡尔坐标的，而clofNet的更新方式是基于局部坐标系 的，其公式表示为：

\(\mathcal{F}_{ij}^{l+1}=\mathrm{EquiFrame}\left(x_i^l,x_j^l\right)\)

\(\boldsymbol{x}_{i}^{l+1}=\boldsymbol{x}_{i}^{l}+\frac{1}{N}\sum_{j\in\mathcal{N}(x_{i})}\mathrm{Vectorize}\left(\boldsymbol{m}_{ij}^{l},\mathcal{F}_{ij}^{l}\right)\)

其中有个关键性操作：向量化，这是标量化的逆操作。具体来说，对于某个位置几何向量\(\mathrm{x}\)在等变框架下的标量化表示\({x^{a},x^{b},x^{c}}\)，我们可以使用这些标量分量与基向量的线性组合重构原始向量，即\(x=x^{a}a+x^{b}b+x^{c}c\)。 这对于从简化的标量表示中恢复复杂的几何结构至关重要，让GMP模块的输出能够直接反映出原始空间中的向量性质，并保持在\(SO(3)\)群下的不变性。在上述公式中，\(x_i^{l+1}\)和\(h_{i}^{l+1}\)便是GMP模块输出的几何向量信息和节点标量信息。

至于消息传递的另一种机制：基于注意力的机制。其灵感主要源于Transformer算法中的Self-attention机制，公式表示如下：

\(\boldsymbol{q}_{i}=\phi_{q}\left(h_{i}^{\prime}\right),\boldsymbol{k}_{ij}=\phi_{k}\left(h_{i}^{\prime},m_{ij}\right),\boldsymbol{v}_{ij}=\phi_{\nu}\left(m_{ij}\right)\)

\(\alpha_{ij}=\frac{\left\langle q_i,k_{ij}\right\rangle}{\sum_{j^{^{\prime}}\in\mathcal{N}(i)}\left\langle q_i,k_{ij}\right\rangle}\)

\(\mathcal{M}_i=\mathrm{LayerNorm}\left(\sum_{j\in\mathcal{N}(i)}\alpha_{ij}\boldsymbol{v}_{ij}\right)\)

\(h_i^{l+1}=\phi_h\left(h_i^l,\mathcal{M}_i\right)\)

\(h_i^{l+1}=h_i^l+\mathrm{LayerNorm}\left(h_i^{l+1}\right)\)

其中：

（1）\(q_{i}\)是查询向量，它由一个多层感知机\(\phi_{q}\)对节点\(\begin{array}{c}{i}\end{array}\)的特征\(h_{i}^{l}\)进行转换得到。

（2）\(k_{ij}\)是键向量，由\(\phi_{k}\)对节点\(\begin{array}{c}{i}\end{array}\)的特征和边\(\text{ij}\)的消息\(m_{ij}\)进行转换得到。

（3） \(v_{ij}\)是值向量，由\(\phi_{v}\)对边\(\text{ij}\)的消息进行转换得到。

（4）\(\alpha_{ij}\)是注意力权重，通过\(q_{i}\)和\(k_{ij}\)的点积计算，然后通过Softmax标准化以确保所有邻居的权重和为1。

（5）\(\mathcal{M}_{i}\)是通过加权求和所有邻居\(\mathrm{j}\)的值向量 \(v_{ij}\)得到的，权重由\(\alpha_{ij}\)给出。

（6）\(h_i^{l+1}\)是新的节点特征，由\(\phi_{h}\)通过结合旧的节点特征和消息汇总\(\mathcal{M}_{i}\)计算得到。

（7）最后，\(h_i^{l+1}\)通过残差连接和层归一化（LayerNorm）更新，以提高训练的稳定性和效率。

注意力机制允许模型集中于最重要的信息，即在图中某个节点的所有邻居中，哪些邻居提供了最重要的信息。这种方法借鉴了Transformer模型在自然语言处理中的成功经验，并将其适用于学习粒子间的复杂相互作用。通过这种方式，ClofNet能够对多体系统进行更精细和灵活的建模。