GraphGAN – 图神经网络公社

在

GraphGAN是一种结合了图神经网络和生成对抗网络（GAN）概念的机器学习模型。它旨在通过对抗学习框架解决图数据中的节点分类和链接预测问题，特别是在缺少标签数据的情况下。GraphGAN通过结合生成器和判别器两个主要组件来学习图中节点的有效表示。

GraphGAN的框架如下：设$G=(V,\mathcal{E})$为一个给定的图，其中$V=\begin{Bmatrix}v_1,\ldots,v_V\end{Bmatrix}$代表顶点的集合，而$\mathcal{E} = \left\{ e_{ij} \right\}_{i,j=1}^{V}$代表边的集合。对于给定的顶点$\nu_{c}$，定义$\mathcal{N}\left(\nu_{c}\right)$为直接连接到$\nu_{c}$的顶点集，也就是顶点$\nu_{c}$的1-hop邻居。我们将顶点$\nu_{c}$的真实连通性分布表示为条件概率$p_{\mathrm{true}}\left(\nu|\nu_{c}\right)$，它反映了$\nu_{c}$的连通性偏好和它所连接顶点的类型。从这个视角来看，$\mathcal{N}\left(\nu_{c}\right)$可以被看作是从$p_{\mathrm{true}}\left(\nu|\nu_{c}\right)$抽取的一组观察样本。给定图$\mathrm{G}$，GraphGAN旨在学习以下两个模型：

生成器$G(\nu|\nu_c;\theta_G)$：尝试近似顶点$\nu_{c}$的真实连通性分布$p_{\mathrm{true}}\left(\nu|\nu_{c}\right)$，并生成（或选择）最有可能与$\nu_{c}$相连接的顶点集。
判别器$D\left(\nu,\nu_{c};\theta_{D}\right)$：旨在鉴别顶点对$\begin{pmatrix}\nu,\nu_{c}\end{pmatrix}$的连通性。$D\left(\nu,\nu_{c};\theta_{D}\right)$输出一个标量值，表示边$\begin{pmatrix}\nu,\nu_{c}\end{pmatrix}$存在的概率。

生成器$\mathrm{G}$和判别器$\mathrm{D}$作为两个对手: 生成器$\mathrm{G}$将试图完美地匹配$p_{\mathrm{true}}\left(\nu|\nu_{c}\right)$并生成类似于$\nu_{c}$的真实直接邻居的相关顶点以欺骗判别器。而判别器$\mathrm{D}$则相反，会尝试检测这些顶点是$\nu_{c}$的真实邻居还是由其对手$\mathrm{G}$生成的。形式上， $\mathrm{G}$和$\mathrm{D}$在一个有以下价值函数$V(G,D)$的双人博弈中进行对抗：

$\min_{\theta_G}\max_{\theta_D}V(G,D)=\sum_{c=1}^V\left(\mathbb{E}_{\nu\sim p_{\mathbf{tne}}(\nu|\nu_c)}\left[\log D(\nu,\nu_c;\theta_D)\right]+\mathbb{E}_{\nu\sim p_G(\nu|\nu_c;\theta_G)}\left[\log\left(1-D(\nu,\nu_c;\theta_D)\right)\right]\right)$ （1）

上式描述的最小最大（Minimax）博弈公式是生成对抗网络的核心。在图生成对抗网络（GraphGAN）的上下文中，生成器$\mathrm{G}$的目标是生成看起来像真实数据的样本。在GraphGAN的情境下，生成器试图生成看似是$\nu_{c}$的1-hop邻居的顶点。而鉴别器$\mathrm{D}$的目标是区分输入样本是来自于真实数据还是生成器生成的假数据。在GraphGAN中，它试图区分一个顶点对$(\nu,\nu_{c})$是否是真实的1-hop邻点对。这个公式包含了两个期望（Expectations）：

第一部分为真实数据的期望$E_{v\sim p_{\mathrm{true}}\left(v\mid v_{c}\right)}\left[\log D\left(v,v_{c};\theta_{D}\right)\right]$。这个期望表示对所有真实的顶点对$\begin{pmatrix}\nu,\nu_{c}\end{pmatrix}$，鉴别器$\mathrm{D}$输出它们是真实邻居的概率的对数。${\mathcal{V}}$是从顶点$\nu_{c}$的真实邻居分布$p_{\mathrm{true}}\left(\nu|\nu_{c}\right)$中采样的。理想情况下: 如果$\nu$确实是$\nu_{c}$的真实邻居，我们希望鉴别器$\mathrm{D}$的输出$D\left(\nu,\nu_{c};\theta_{D}\right)$接近于1 (最大的可能性)。此时$\log D\left(\nu,\nu_{c};\theta_{D}\right)$会接近0（因为$\log(1){=}0$）。

第二部分是关于生成数据的期望$E_{\nu\sim p_G\left(\nu|\nu_c;\theta_G\right)}\left[\log\left(1-D\left(\nu,\nu_c;\theta_D\right)\right)\right]$。这个期望表示对所有生成器$\mathrm{G}$生成的顶点对$\begin{pmatrix}\nu,\nu_{c}\end{pmatrix}$，鉴别器$\mathrm{D}$输出它们不是真实邻居的概率的对数。$\nu$是从生成器$\mathrm{G}$的分布$p_{G}\left(\nu|\nu_{c};\theta_{G}\right)$中采样的。理想情况下：如果$\nu$是生成器$\mathrm{G}$生成的，并不是$\nu_{c}$的真实邻居，我们希望判别器$\mathrm{D}$的输出$D\left(\nu,\nu_{c};\theta_{D}\right)$接近于0。此时, $\log\left(1-D\left(\nu,\nu_c;\theta_D\right)\right)$也会接近0（因为$\log(1-0)=0$）。

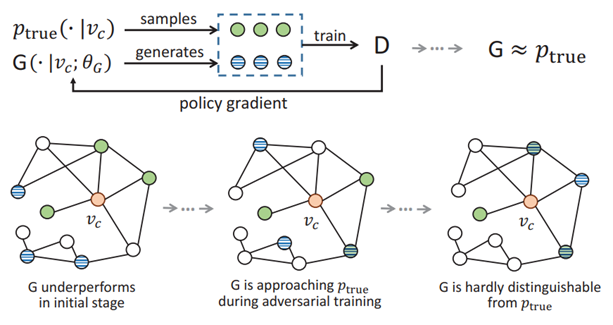
可以看出这两部分期望的目标都是希望经过训练后，其值越来越小，理想情况下为0，因此可以看作GraphGAN的损失函数，GraphGAN的训练状态如图1所示。

阴影的圆代表从真实图结构中采样的真实与顶点$\nu_{c}$连接的邻居，横条纹的圆代表生成器认为的应该与$\nu_{c}$连接的邻居。在训练的初始阶段（左图），生成器$\mathrm{G}$的表现并不佳，其生成的顶点与实际的邻居相比，差异较大，很容易被鉴别器$\mathrm{D}$区分。随着对抗训练的进行（中图），生成器$\mathrm{G}$逐渐学习到更好的生成策略，使得生成的邻居和实际的邻居更难以区分。在经过充分的训练之后，生成器$\mathrm{G}$生成的邻居与实际的邻居非常接近，即右图中，阴影的圆和横条纹的圆存在大量重叠。鉴别器$\mathrm{D}$几乎无法区分。在这个博弈中，鉴别器尽量提高识别真实和生成数据对的准确性，而生成器尽量生成看起来越真实的数据。通过这种对立的训练过程，两个模型都在不断改进，直到达到一个平衡点，即生成器生成的数据非常逼真，鉴别器很难区分真假数据对。

下面具体的讲解GraphGAN的优化过程，对于判别器而言，定义鉴别器$\mathrm{D}$的输出为两个输入顶点$(\nu,\nu_{c})$内积的Sigmoid函数：

$D\left(\nu,\nu_c\right)=\sigma\left(d_\nu^\top d_{\nu_c}\right)=\frac{1}{1+\exp\left(-d_\nu^\top d_{\nu_c}\right)}$ （2）

定义$\theta_{D}$是判别器的可学习参数。任何具有区分能力的模型都可以在此作为$\mathrm{D}$，例如一个神经网络模型，对顶点$\nu$和$\nu_{c}$的特征向量进行学习映射后得到的$\mathrm{k}$维新的向量表示为$d_{\nu},d_{\nu_{c}}$，然后进行内积和Sigmoid处理。这个内积表示了两个顶点之间的相似性或关系强度。内积的结果通过Sigmoid函数进行处理，得到一个在0到1之间的值，可以解释为顶点对$\nu$和$\nu_{c}$是图中真实连接的概率。其中$\nu$的采样有两种情况，换句话说，判别器随机接收两类输入数据（$\nu\sim p_{\mathrm{true}}$或$\nu\sim G$）。根据损失函数公式(1)，判别器的梯度$\nabla_{\theta_{D}}V(G,D)$计算如下：

$\nabla_{\theta_D}V(G,D)=\begin{cases}\nabla_{\theta_D}\log D\left(\nu,\nu_c\right),\mathrm{~if~}\nu\sim p_\mathrm{true}\\\nabla_{\theta_D}\left(1-\log D\left(\nu,\nu_c\right)\right),\mathrm{~if~}\nu\sim G.&&\end{cases}$ （3）

在训练过程中，GraphGAN交替地更新生成器$\mathrm{G}$和判别器$\mathrm{D}$的参数，以便最小化生成器的损失函数和最大化判别器的损失函数，这个过程通常被称为对抗训练。式(3)便是固定生成器$\mathrm{G}$更新判别器$\mathrm{D}$时，判别器的梯度计算方法。

类似的，生成器$\mathrm{G}$具体的模型类型也没有限制，GCN、GAT甚至简单的神经网络等等都可以，只要能具备预测某顶点与其他顶点间连接概率的能力即可。当固定判别器$\mathrm{D}$，更新生成器$\mathrm{G}$的参数时，式(1)中的$E_{\nu\sim p_{\mathrm{true}}(\cdot\mid\nu_{c})}\left[\log D\left(\nu,\nu_{c};\theta_{D}\right)\right]$部分可以看作常数，只需要关注另一部分，即$\left.E_{\nu\sim G\left(\cdot\mid\nu_c;\theta_G\right)}\left[\log\left(1-D\left(\nu,\nu_c;\theta_D\right)\right)\right]\right)$。此时，生成器的梯度$\nabla_{\theta_{G}}V(G,D)$为：

$\begin{aligned}\nabla_{\theta_{G}}V(G,D)&=\nabla_{\theta_G}\sum_{c=1}^{V}E_{\nu\sim G\left(\cdot\mid\nu_c\right)}\left[\log\left(1-D\left(\nu,\nu_c\right)\right)\right]\\&=\sum_{c=1}^V\sum_{i=1}^N\nabla_{\theta_G}G\left(\nu_i|\nu_c\right)\mathrm{log}\left(1-D\left(\nu_i,\nu_c\right)\right)\\&=\sum_{c=1}^V\sum_{i=1}^NG\left(\nu_i|\nu_c\right)\nabla_{\theta_G}\log G\left(\nu_i|\nu_c\right)\log\left(1-D\left(\nu_i,\nu_c\right)\right)\\&=\sum_{c=1}^V\mathbb{E}_{\nu\sim G\left(\cdot|\nu_c\right)}\left[\nabla_{\theta_G}\log G\left(\nu|\nu_c\right)\mathrm{log}\left(1-D\left(\nu,\nu_c\right)\right)\right]\end{aligned}$ （4）

在式(4)的推导中，$\sum_{c=1}^VE_{\nu\sim G(\cdot\nu_c)}\left[\log\left(1-D\left(\nu,\nu_c\right)\right)\right]$是对所有顶点$\nu_{c}$的期望求和，其中每个期望是从生成器$\mathrm{G}$生成的顶点$\nu$对应的$\log\left(1-D\left(\nu,\nu_c\right)\right)$的平均值。这表明我们在考虑所有生成器产生的假顶点与真实顶点$\nu_{c}$之间关系的平均对数概率。期望的实现可以转化成对每个生成样本的求和，即$\sum_{i=1}^N\nabla_{\theta_G}G\left(\nu_i|\nu_c\right)\log\left(1-D\left(\nu_i,\nu_c\right)\right)$，这里对每个生成样本${\mathcal{V}}_{i}$求和，计算生成概率相对于$\theta_{G}$的梯度与$\log\left(1-D\left(\nu_i,\nu_c\right)\right)$的乘积。又因为概率的梯度可以写作概率乘以似然比例的梯度，因此可以使用$G\left(\nu_i|\nu_c\right)\nabla_{\theta_G}\log G\left(\nu_i|\nu_c\right)\mathrm{log}\left(1-D\left(\nu_i,\nu_c\right)\right)$代替$\nabla_{\theta_G}G\left(\nu_i|\nu_c\right)\mathrm{log}\left(1-D\left(\nu_i,\nu_c\right)\right)$。最后，我们用期望值来代替求和，因为期望值是随机变量的平均值，这里的随机变量是$\nu$的生成概率，得到推导后生成器的梯度计算公式：$E_{\nu\sim G(\cdot\mid\nu_c)}\left[\nabla_{\theta_G}\log G\left(\nu|\nu_c\right)\mathrm{log}\left(1-D\left(\nu,\nu_c\right)\right)\right]$。整体上，这个梯度表达式说明：为了更新生成器$\mathrm{G}$的参数，我们需要考虑由$\mathrm{G}$生成的每个顶点$\mathrm{v}$对损失函数的贡献，并根据该贡献来调整$\theta_{G}$。梯度的方向指示了如何更新参数$\theta_{G}$以减少生成的顶点$\mathrm{v}$被判别器$\mathrm{D}$识别出的概率，从而使生成器产生更真实的样本。

值得注意的是，在给定顶点$\nu_{c}$时，生成器$\mathrm{G}$计算其他顶点与$\nu_{c}$的连通性概率$G\left(\nu|\nu_{c}\right)$需要使用Softmax函数计算出$\nu_{c}$外的所以节点。公式如下所示：

$G\left(v|v_c\right)=\frac{\exp\left(g_v^\top g_{v_c}\right)}{\sum_{v\neq v_c}\exp\left(g_v^\top g_{v_c}\right)}$ （5）

当图数据体量庞大时，上述公式的计算复杂度是非常高的。因此，在GraphGAN框架中，提出了一种称为Graph Softmax的新方法，它的核心思想有三点：

（1）规范化（Normalized）：生成器应该产生一个有效的概率分布，这意味着对于一个给定的顶点$\nu_{c}$，所有可能与之相连的顶点$\mathrm{v}$的生成概率之和应该等于1，这也是Softmax函数的基本思想。

（2）图结构意识（Graph-structure-aware）：生成器在确定顶点之间的连通性概率时，应该利用图的结构信息。具体来说，如果两个顶点之间的最短路径距离增加，它们被认为是相连的概率应该下降。

（3）计算效率（Computationally Efficient）：与Softmax不同，Graph Softmax在计算时只考虑图中少数的特定顶点，从而提高计算效率。

为了实现Graph Softmax，首先需要执行一个从顶点$\nu_{c}$出发的广度优先搜索（Breadth-First Search，BFS），来构建一棵以$\nu_{c}$为根的BFS树$T_{c}$。使用这棵树，我们可以计算每个邻居顶点$\nu_{i}$相对于$\nu_{c}$的相关性概率$p_{c}\left(\nu_{i}\right)$，这是一个标准的Softmax函数，它在$\nu_{c}$的直接邻居集$N_{c}(\nu)$上运算。接着，为了计算任意顶点$\nu$与$\nu_{c}$之间的连通性概率$G\left(\nu|\nu_c;\theta_G\right)$，我们使用$T_{c}$中从$\nu_{c}$到$\nu$的唯一路径。路径上每对相邻顶点的相关性概率的乘积定义了$\nu$和$\nu_{c}$之间的连通性概率。通过这种方式，图Softmax只关注$\nu_{c}$通过BFS可达的部分图，而不是整个图，这极大地提高了计算效率。同时，它也自然地考虑到了图的结构信息，因为它直接在BFS树上进行操作，这棵树反映了图中顶点之间的真实距离关系。因此这种方法是规范化的，具有图结构意识，且计算效率高，具体示例如图2所示。

如图2所示，从顶点$\nu_{c}$开始，我们有原始的图$\mathrm{G}$和一个以$\nu_{c}$为根节点的 BFS 树。第一步是从$\nu_{c}$的直接邻居中选择下一个顶点。在这个例子中，顶点$\nu_{r1}$被选中，与它相关联的概率是0.7。接下来，从$\nu_{r1}$的邻居中选择下一个顶点。顶点$\nu_{r2}$被选中，与它相关联的概率是 0.3。然后，从$\nu_{r2}$的邻居中选择下一个顶点。可能的选择只有两种，与它们相关联的概率是 0.6和0.4，假设此时以0.6的概率选择了$\nu_{r1}$，那么$\nu_{r2}$的路径采样过程完成，否则路径采样继续延续。最后一步是更新采样路径上所有顶点的概率。计算路径$\nu_{c}\to\nu_{r1}\to\nu_{r2}$上所有顶点的相关性概率的乘积得到0.7×0.3×0.6=0.126 ，这个数字代表从$\nu_{c}$到$\nu_{r2}$的连通性概率。